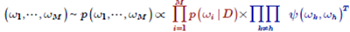統計数理研究所吉田亮研究室

バイオサイエンスの統計学：ゲノム、分子・システム設計、バイオイメージング

本研究室は，ベイズ統計学と機械学習を駆動力として，バイオサイエンス分野の諸問題に幅広く取り組んでいます．ここでは，以下の四つの研究課題を紹介します．
(1) 力学的反発力に基づく並列型マルコフ連鎖モンテカルロ法とゲノム配列のパターン認識（池端久貴・総研大; 吉田亮・統計数理研究所）
(2) カーネル原像法による有機化合物の分子設計（山下博史・総研大; 伊庭幸人樋口知之・統計数理研究所; 磯村哲・(株)地球快適化インスティチュート; 吉田亮・統計数理研究所）
(3) 4次元顕微鏡画像に基づく神経細胞のカルシウムイオン濃度の定量化（徳永旭将逸見昌之・統計数理研究所; 飯野雄一・東京大学; 石原健・九州大学; 岩崎唯史・茨城大学; 広瀬修・金沢大学; 池端久貴・総研大; 吉田亮・統計数理研究所）
(4) ベイジアン・モデリング技術を使った生体分子ネットワークの構造設計と制御

大量の文字列からモチーフを発見する問題とベイズ統計学

科研費・新学術領域研究「システムがん」公募研究：「第二世代モチーフ解析法に基づくがん細胞に特異的な転写制御経路の発見」（研究代表者：吉田　亮）

次世代シーケンサ技術の普及により、ゲノム情報のデータ量が爆発的に増大し、データ解析の方法論に抜本的な見直しが求められている.モチーフ配列の発見、すなわち塩基配列に埋め込まれた短い保存配列を検出する問題は,生物情報学の創生期からの研究対象であり,これまでに多くの方法論が提唱されてきた.しかしながら,近年のデータの大規模化に際し,これら第一世代のモチーフ検出法はその機能を果たせなくなりつつある.第一世代アルゴリズムには,長さ10³bp,配列数のオーダーで10²程度のデータサイズしか想定されておらず,計算速度と性能の両面でデータの増加に対し全くスケーリングできない.そこで,第二世代アルゴリズムの開発競争が始まることになる.本研究は,力学的反発力に基づく並列型マルコフ連鎖モンテカルロ法（MCMC）を開発し,世界最高水準の第二世代アルゴリズムを完成させることを目指す.

Repulsive parallel MCMC(RPMCMC)アルゴリズム:従来法の重大な欠点は,局所解へのトラップである.初期条件を変更し,サンプリングを複数回実行しても,情報量過多の同じ疑似モチーフにトラップしてしまう.疑似モチーフは,反復配列やGC含有量が異常に高い,応用上の価値が低いものである.PRMCMCは,単純なアイデアで,この欠点を克服する:複数のアルゴリズムを並列に実行する際,サンプリングの軌道に「反発作用」を与え,各々が異なるモチーフ配列に到達するように作業分担させる.このタスク分割機能により,一回の並列計算で多様なモチーフ配列を重複なく検出できるようになる.

事後分布のM個のレプリカを作り,反発作用を加える.Ψは反発関数,Τは温度パラメータ.温度を下げながら,この拡大事後分布からM本のサンプル列を生成する.

p_image13

カーネル法に基づく創薬支援システムの開発

科研費・挑戦的萌芽研究：「機械学習に基づく新しい創薬インフォマティクス－医薬品化合物の分子設計」（研究代表者：吉田　亮）

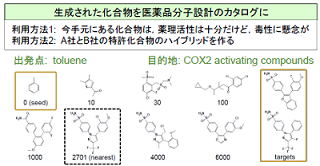
本研究室では，カーネル法に基づくドラッグデザインの手法を開発している．とりわけ，次の３つの研究課題に取り組んでいる：(1)化学構造カーネル（グラフカーネル）の設計，(2)医薬品候補の化学構造から薬理活性や毒性を予測する判別機の開発，(3)カーネル原像問題に基づく化合物の構造改変手法の開発

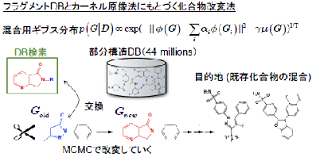
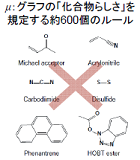
化合物の化学構造を縮約表現するツールとして,グラフカーネルの設計に取り組んでいる.化学構造カーネルの設計は,個々の化合物をラベル付きグラフで表現することから始まる.カーネル関数は,二つの化合物に内在する共通の部分構造を数え上げ,化合物の類似度を評価するものである.当該分野におけるカーネル関数の研究開発は1990年代後半から始まり,これまでに数種類の標準手法が確立している.しかしながら,従来のカーネル関数の多くは,完全に一致する部分構造のみ数え上げるように設計されており,数原子のミスマッチがある構造は類似度にカウントされないという欠点がある.このことが機能予測の性能低下の一因となっている.そこで,構造の完全一致という制約を緩和するより柔軟なカーネル関数を開発し,化学構造からその性質を予測するためのモデル作りに取り組んでいる.

医薬品開発のもう一つの研究課題は,ある化学的性質を満たす化合構造を設計することである.既存化合物のアッセイデータから予測モデルを構築する過程で,性質に特異的な化学構造が得られる.このように得られた複数の構造をブレンドし,新規の化合物を設計する.
アイデアは単純である.混合対象の化学構造を特徴空間で結合し,ギブス分布のポテンシャル関数に新規化合物と混在構造のノルムをセットする.このギブス分布からラベル付き無向グラフをサンプリングすることで,混合構造の内点付近にどのような化合物が分布しているかを知ることができる.われわれはフラグメント・フリップMCMC法という手法を開発し,化合物グラフのランダム・サンプリングを実現した.

４次元顕微鏡動画に基づく神経細胞のカルシウムイオン分布の定量化

JST/CREST「生命動態の理解と制御のための基盤技術の創出」：「神経系まるごとの観測データに基づく神経回路の動作特性の抽出」（研究代表者：飯野　雄一）

線虫C.elegansの神経系は,302個の神経細胞から構成され,全てのシナプス結合の構造が明らかになっている.4D（空間3次元+時間1次元）カルシウムイメージング技術を利用して,複数の「生きた」神経細胞の活動状態を同時に測定することで,神経系による空間認識や運動制御,化学走性など,神経回路の動作原理を明らかにすることを目指している.

神経細胞のカルシウムイオン濃度の時空間分布を顕微鏡で計測し,取得された動画像から個々の細胞の神経活動を定量化する.画像内のオブジェクト（細胞体）は高密度に分布し,形状は不均一,さらには時空間的な変化を伴う.このような画像情報から細胞の個数を数え上げ,位置を同定し,オブジェクトの時空間変化を追跡するという問題に取り組んでいる.

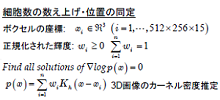生体分子ネットワークの逆問題：ロバストなネットワークを設計する

遺伝子発現・シグナル伝達・代謝反応など、細胞プログラムの本質的な機能は生体分子の相互作用ネットワークに書き込まれています。本研究室では、生体分子ネットワークの動作・設計原理の解明に役立つバイオモデリング技術とデータ解析手法の開発を行っています。ここでは一例として、細胞のロバスト性に関する研究を紹介します。
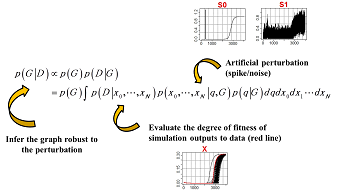
生物は様々な外的変化に柔軟に対応しながら、生命システム全体の安定性や恒常性を維持しています。例えば、外界温度や生化学パラメータの変化に対して、個々の素過程は高い揺らぎを示しますが、生物の発生や分化のプログラムは驚くほど厳密な規則性を保ちながら正確に遂行されます。近年の分子生物学の研究は、生命システムのロバスト性を維持するメカニズムとして、(1) 反応経路の冗長性; (2) 生化学物質の冗長性; (3) ネットワークの構造的安定性; (4) モジュール性などを明らかにしてきました。
本研究室では、このようなロバストなネットワーク・システムを自動設計するためのモデリング手法の開発を行っています。技術基盤は階層ベイズのモデル設計原理と確率的なグラフ探索アルゴリズムが礎となっています。直観的に説明すると、次のようになります：システムに任意の摂動を与えたもとで、ベイズ的なモデル設計規準に従ってモデル(ネットワーク構造)を改変していくことで、摂動の影響を緩和しつつ観測されたデータを安定的に再現できるロバストなネットワーク・システムを得ることが可能ということです。このような技術は、ロバスト性の維持に関わるネットワーク・モチーフの発見や代謝経路の工学設計に応用することができます。

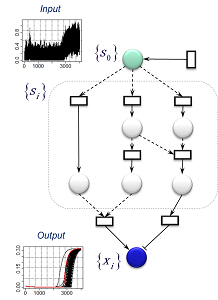
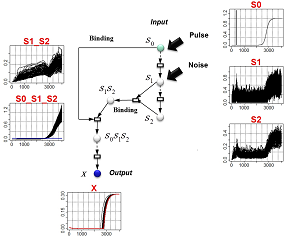
ベイズ統計学のモデル設計原理とロバスト性の関係：システムの摂動をモデル化した上で、モデルの事後確率が高くなるようにネットワーク・システムの構造Gを改変していけば、摂動の影響を取り除きながらデータのパターンDを安定的に再現できるモデルを自動構築することができる

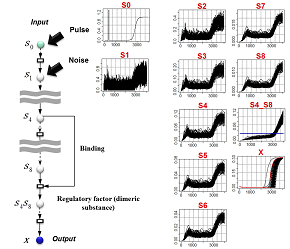
例：入力シグナルにパルス＋ノイズを与えたもとで、出力Xの反応遅延と位相の揺らぎを同時に除去できるネットワーク構造を設計する。(赤：観測データ)

推定されたネットワーク構造：左のモデルの主要構成因子は、直列に連結された8個の中間変数によるシグナル伝達経路である。これに加え、二つの中間変数が複合体を形成し、これが出力Xを最終的に制御している。出力Xのパターンを見ると、摂動の影響をある程度吸収することができているが、Xの発火タイミングは元のシグナルに比べて遅延傾向にある。これに対して右のモデルは、摂動に対してロバストであると同時にシグナルのタイミングを正しくXに伝達している。