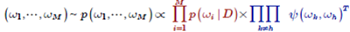Ryo Yoshida Lab

Bioscience Statistics: Genomics, Molecular Design, and Biological Image Mining

Our laboratory applies the powerful tools of Bayesian statistics and machine learning to address a wide variety of problems in the biosciences. In this poster, we present three of the primary focus areas of our research:
(1) Parallel Markov-chain Monte Carlo methods based on mechanical repulsive forces and pattern recognition in genome sequencing(Hisaki Ikebata, Graduate University for Advanced Studies; Ryo Yoshida, Institute of Statistical Mathematics)
(2) Molecular design of organic compounds via the kernel pre-image method（Hiroshi Yamashita, Graduate University for Advanced Studies; Yukito Iba and Tomoyuki Higuchi, Institute of Statistical Mathematics; Tetsu Isomura, The KAITEKI Institute; Ryo Yoshida, Institute of Statistical Mathematics）
(3) Using four-dimensional microscopic imaging to quantify the calcium ion concentrations in nerve cells（Terumasa Tokunaga and Masayuki Henmi, Institute of Statistical Mathematics; Yuuichi Iino, Tokyo University; Takeshi Ishihara, Kyushu University; Yuishi Iwasaki, Ibaraki University; Osamu Hirose, Kanazawa University; Hisaki Ikebata, Graduate University for Advanced Studies; Ryo Yoshida, Institute of Statistical Mathematics）
(4) The inverse problem in biomolecular networks: Designing robust networks

Bayesian statistics and the problem of detecting motifs in huge character strings

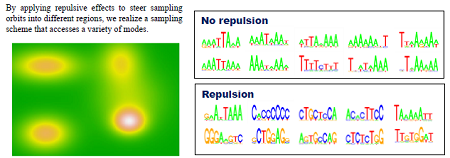
The spread of next-generation sequencer technology has created an explosion in the quantity of genomic data to analyze, and this in turn has necessitated a radical rethinking of the theoretical methodology for analyzing such data. Motif sequence detection (the problem of finding short conserved sequences buried in long base sequences) has been a focus of research in bioinformatics ever since the birth of the field, and many methodologies have been proposed to date. However, as the datasets have become massive in recent years, the first-generation motif-detection techniques have become less able to fulfill their required function. First-generation algorithms were only expected to deal with data of length up to 103 base pairs, or in terms of sequences, around 102, and are totally incapable of being scaled up in terms of both performance and computation time to accommodate the increase in data. This sets the stage for competition to develop second-generation algorithms. In this research, we develop a parallel Markov-chain Monte Carlo (MCMC) method based on mechanical repulsive forces, with aspirations to achieve a second-generation algorithm meeting the highest global standards.

Repulsive parallel MCMC (RPMCMC) algorithm: A major disadvantage of traditional methods is that they tend to get trapped in local solutions. Even upon multiple sampling runs with varied initial conditions, many methods get trapped at false motifs exhibiting the same degree of data overload. These false motifs tend to have extremely high concentrations of GC and many repeated sequences, and are of little practical value. The RPMCMC method employs a simple idea for overcoming this difficulty: we run multiple algorithms in parallel, apply “repulsive effects” to the sampling orbits, and use a division-of-labor scheme in which each run ultimately arrives at a distinct destination motif. The multitasking character of this algorithm allows a single parallel computation to detect a variety of motif sequences with no duplication.

We create M replicas of the posterior distribution and add repulsive effects.Ψ is the repulsion function.Τ is a temperature parameter. We produce M sample chains from this enlarged posterior distribution while reducing the temperature.

p_image13

Development of drug-design support systems based on the kernel method

Our laboratory develops drug-design techniques based on the kernel method. In particular, we are involved in the following three research projects: (1) designing chemical structure kernels (graph kernels), (2) developing identification instruments to predict the pharmacological activity and toxicity of pharmaceutical candidates based on their chemical structures, and (3) developing methods for modifying the structure of compounds based on the kernel pre-image problem.

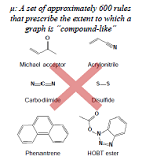
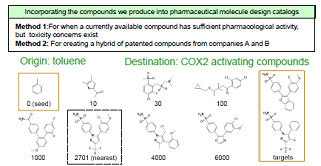
As a tool for obtaining a reduced representation of the chemical structure of a compound, we are addressing the design of graph kernels. The design of chemical structure kernels begins by expressing each of the individual compounds in the form of a labeled graph. The kernel function then counts the common substructures present in two distinct compounds and assesses the degree of similarity between the compounds. Research and development into kernel functions for various relevant fields began in the late 1990s, and by now several standard methods have been established. However, most kernel functions that have been used to date are designed to count only cases of perfect agreement between substructures; this has the undesirable consequence that structures with minor mismatches of even just a few atoms will not be counted as similar. This is one factor underlying the declining performance of functional prediction. To address this difficulty, we are developing more flexible kernel functions that relax the restriction of complete agreement between structures as a step toward the design of models to predict the properties of compounds from their chemical structure.

Another research problem in pharmaceutical development is the challenge of designing a chemical structure that exhibits given chemical properties. In the process of building predictive models from assay data on existing compounds, one obtains chemical structures with unique properties. By blending several such structures obtained in this way, we design new compounds. The idea here is simple: The chemical structures to be blended are conjoined in feature space, and the norms of the new compound and the blended structure are set as the potential function of a Gibbs distribution. Then sampling a labeled undirected graph from this Gibbs distribution allows us to learn what sorts of compounds are distributed in the vicinity of interior points within the blended structure. We have developed a method known as the “fragment flipping” MCMC method to perform random sampling of graphs of chemical compounds.

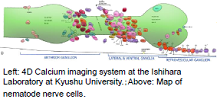
Using four-dimensional microscopic video to quantify the calcium ion distribution in nerve cells

The nervous system of the nematode C. elegans is composed of 302 nerve cells, and the structure of all of the synapse connections is fully known. Our goal is to use four-dimensional (three spatial dimensions plus one time dimension) calcium-imaging technology to simultaneously measure the activity states of multiple live nerve cells, and thereby elucidate the operating principles of the nervous circuitry, including spatial recognition and motor control by the nervous system, and the chemotactic properties.

We use a microscope to measure the spatiotemporal distribution of the calcium ion concentrations in nerve cells, and then use the video thus obtained to quantify the nervous activity states of individual cells. Objects (cell bodies) in the images are distributed with high density, have non-uniform shapes, and exhibit spatiotemporal variations. We are currently studying the problem of how to use such image data to count the number of cells, to identify the positions of cells, and to track the spatiotemporal changes demonstrated by objects.

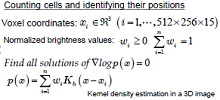The Inverse Problem in Biomolecular Networks: Designing Robust Networks

The essential functions of cellular programs, such as gene expression, signal transmission, and metabolic reactions, are encoded in the interaction networks of biomolecules. Our laboratory develops biomodeling technology and data-analysis techniques that are useful for elucidating the operation of, as well as the design principles underlying, biomolecular networks. As an example, we here present our research on cellular robustness.

Lifeforms maintain the stability and homeostasis of their entire life system even as they adapt flexibly to a variety of external changes. For example, their individual elementary processes display a high degree of fluctuation with respect to changes in the temperature of the outside world or in other biochemical parameters, yet the programs for the emergence and differentiation of life continue nonetheless to be accurately executed, preserving a surprisingly high degree of strict regularity. In recent years, molecular biology research has uncovered several mechanisms for maintaining robustness in life systems, including (1) redundancy of reaction pathways, (2) redundancy in biochemical substances, (3) structural stability of networks, and (4) modularity.

Our laboratory is developing modeling techniques to automate the design of these types of robust network systems. The technical foundations of our efforts are rooted in hierarchical Bayesian model design principles and probabilistic graph-search algorithms. A simple intuitive description of this branch of our research is as follows: Subjecting a system to an arbitrary external perturbation enables us, by adapting the system model (the network structure) in accordance with Bayesian model-design criteria, to obtain robust networks and systems capable of stably reproducing observed data while simultaneously mitigating the impact of the disruption. This sort of technology may be applied to the discovery of network motifs responsible for ensuring robustness, as well as to the engineering design of metabolic pathways.

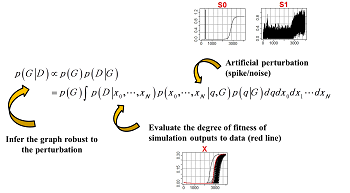
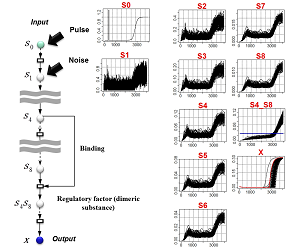
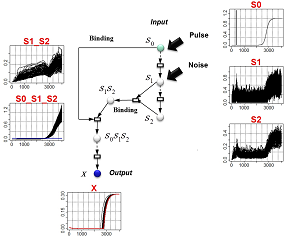
Relationship between Bayesian-statistical model-design principles and robustness:By modeling the perturbation of a system and then adapting the structure (G) of the network system in such a way that the model's posterior probabilities are high, it is possible to automate the design of models capable of reliably reproducing the data pattern (D) while eliminating the influence of the perturbation.

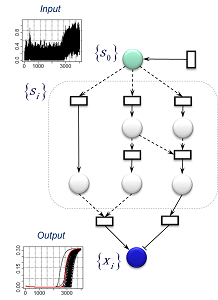
Example: By considering the addition of a pulse plus noise to a given input signal, we design network structures capable of simultaneously eliminating both the response delay and the phase fluctuations in the output X. (Red: measured data)

Inference of network structure：The primary structural element of the model at left is a signal-transmission pathway consisting of eight series-connected intermediate variables. In addition, two of the intermediate variables combine to form a compound body which ultimately controls the output X. A glance at the pattern of output X reveals that, although the influence of the perturbation has been absorbed to some extent, the timing of the firing of the X signal tends to be delayed with respect to the original signal. In contrast, the model at right is not only robust with respect to perturbations, but also properly transmits the timing of the original signal through to the output X.